เมื่อฉันเริ่มทำงานในตลาดการเงิน ผู้ค้าตราสารหนี้เป็นเด็กที่ยอดเยี่ยม พวกหุ้นขับ Maseratis และทำตัวเหมือนตัวตลก แต่พวกหุ้นบอนด์ขับสไตล์ที่มีเหตุผลอย่าง Mercedes และสนใจเรื่องต่างๆ เช่น การขาดดุลและเครดิต คำที่เชื่อถือได้ในเรื่องนี้มาจากหนังสือ โป๊กเกอร์ของคนโกหก โดย Michael Lewis เกี่ยวกับ Salomon Brothers ในปี 1980 ซึ่งผู้เข้ารับการฝึกอบรมกลัวว่าจะถูกมอบหมายให้ทำ ตราสารทุนในดัลลัส.
ในตอนนั้น พวกหุ้นกังวลเกี่ยวกับรายได้ คุณภาพของการจัดการและงบดุล และคนที่น่าเบื่อจริงๆ กังวลเกี่ยวกับส่วนต่างของความปลอดภัยและการลงทุนในราคาที่เหมาะสม ตอนนี้ดูเหมือนวิคตอเรีย แต่ฉันเดาว่าความคิดที่ว่าสถาบันเงียบขรึมควรเป็นเจ้าของพันธบัตรเท่านั้น
รายการความกังวลที่ลดลง แต่ยังคงมีอยู่คืออัตราดอกเบี้ย Ol’ Marty Zweig เคยมีโฆษณาชิ้นหนึ่งที่เขากล่าวว่า “หากคุณมองเห็นการเปลี่ยนแปลงที่มีความหมาย (ไม่ใช่แค่การซิกแซก) ในอัตราดอกเบี้ยและโมเมนตัม คุณจะอยู่ในหุ้นเป็นส่วนใหญ่ในช่วงที่มีความก้าวหน้าครั้งใหญ่และออกในช่วงที่ตกต่ำครั้งใหญ่” เหตุผลที่อัตราดอกเบี้ยมีความสำคัญต่อนักเล่นหุ้นก็คือ มูลค่าปัจจุบันของชุดของกระแสเงินสด เช่น เงินปันผล ขึ้นอยู่กับอัตราดอกเบี้ยที่ใช้คิดลดกระแสเงินสดเหล่านั้น
โดยทั่วไป หากเส้นโค้งส่วนลด (เส้นอัตราผลตอบแทน) แบนราบ มูลค่าปัจจุบัน (PV) ของชุดกระแสเงินสด (CF) คือผลรวมของมูลค่าปัจจุบันของกระแสเงินสดแต่ละรายการ:
…ที่ไหน ร คืออัตราดอกเบี้ย
ในกรณีพิเศษ หากกระแสเงินสดทั้งหมดเท่ากันและดำเนินต่อไปตลอดไป เราจะมีค่าคงที่โดยที่ PV = CF/r โปรดทราบว่าหากกระแสเงินสดทั้งหมดมีมูลค่าจริงเท่ากันและปรับเฉพาะสำหรับ เงินเฟ้อและตัวส่วนคือ a จริง อัตราดอกเบี้ย แล้วคุณจะได้คำตอบเดียวกันสำหรับปัญหาตลอดกาล[1]
ฉันควรจะพูดตอนนี้ว่า ประเด็นของบทความนี้ไม่ได้อยู่ที่การสร้าง Gordon Growth Model หรือโต้แย้งว่าคุณควรกำหนดราคาของบางอย่างที่อัตราการเติบโตสูงกว่าอัตราคิดลดอย่างไร หรือวิธีที่คุณปฏิบัติต่ออัตราติดลบใน แบบที่ไม่ทำให้หัวแตก ประเด็นของบทความนี้เป็นเพียงเพื่อแสดงให้เห็นว่าความอ่อนไหวของมูลค่าปัจจุบันที่มีต่อตัวเศษและตัวส่วนเปลี่ยนแปลงไปอย่างไรเมื่ออัตราดอกเบี้ยเปลี่ยนแปลง
ความไวต่อตัวเศษเป็นเรื่องง่าย PV เป็นเส้นตรงเมื่อเทียบกับ CF นั่นคือ ถ้ากระแสเงินสดเพิ่มขึ้น $1 ต่องวด มูลค่าปัจจุบันของทั้งชุดจะเพิ่มขึ้นเท่ากันโดยไม่คำนึงว่าเราจะเพิ่มจาก $2 เป็น $3 หรือ $200 เป็น $201 ในตารางด้านล่าง คอลัมน์ด้านซ้ายสองคอลัมน์แสดงค่าของค่าความเป็นอมตะ $5 เทียบกับค่าความเป็นอมตะ $6 ที่อัตราดอกเบี้ยต่างๆ คอลัมน์ด้านขวาสองคอลัมน์แสดงค่าของค่าความเป็นอมตะ $101 เทียบกับค่าความเป็นอมตะ $102 คุณจะเห็นว่าในแต่ละกรณี ค่าของความเป็นนิรันดร์จะเพิ่มขึ้นในจำนวนเดียวกันจากซ้ายไปขวาในคอลัมน์สีเขียว เช่นเดียวกับที่เพิ่มจากซ้ายไปขวาในคอลัมน์สีน้ำเงิน ตัวอย่างเช่น หากอัตราดอกเบี้ยอยู่ที่ 5% การเพิ่มขึ้นของ $1 จะเพิ่มมูลค่ารวม $20 ไม่ว่าจะเป็นจาก $5 เป็น $6 หรือ $100 เป็น $101
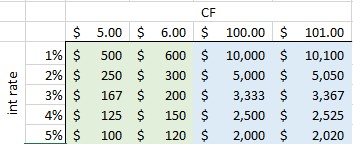
คุณค่าของความเป็นอมตะ
อย่างไรก็ตาม ผลของการเคลื่อนไหวที่มีขนาดเท่ากันในตัวส่วนนั้นแตกต่างกันมาก เราเรียกสิ่งนี้ว่าความอ่อนไหวต่ออัตราดอกเบี้ย ระยะเวลา, และในรูปแบบหนึ่งความไวนั้นถูกกำหนดให้เป็นการเปลี่ยนแปลงของราคาสำหรับการเปลี่ยนแปลง 1% ของอัตราผลตอบแทน[2]
การย้ายจาก 1% เป็น 2% จะลดมูลค่าของเงินรายปี (ในทุกกรณี) ลง 50% แต่การย้ายจาก 4% เป็น 5% จะลดมูลค่าลงเพียง 20%
สิ่งนี้หมายความว่าหากอัตราดอกเบี้ยต่ำ แสดงว่าคุณสนใจอัตราดอกเบี้ยมาก การเปลี่ยนแปลงตัวเศษของคุณจะถูกลบออกอย่างง่ายดายด้วยการเปลี่ยนแปลงเล็กน้อยในอัตราดอกเบี้ยที่คุณกำลังคิดลด แต่เมื่ออัตราดอกเบี้ยสูงขึ้น สิ่งนี้จะมีความสำคัญน้อยลงและคุณสามารถเน้นที่ตัวเศษได้มากขึ้น แน่นอน ในกรณีนี้ เราถือว่าตัวเศษไม่เปลี่ยนแปลง แต่สมมติว่ามันเปลี่ยน? ความสำคัญของการเปลี่ยนแปลงในตัวเศษไม่ได้ขึ้นอยู่กับตัวเศษ แต่ขึ้นอยู่กับตัวส่วน และสำหรับก ที่ให้ไว้ ตัวเศษ การเปลี่ยนแปลงใดๆ ในตัวส่วนจะมีความสำคัญมากขึ้นในอัตราที่ต่ำ
แล้วฉันจะไปที่ไหนกับเรื่องนี้?
ลองนึกถึงตลาดหุ้น เป็นเวลาหลายปีแล้วที่ตลาดหุ้นทำราวกับว่าเฟดทำ ไกล สำคัญกว่าสิ่งที่ธุรกิจทำ และคุณรู้อะไรไหม นักลงทุนอาจมีเหตุผลในการทำเช่นนั้น ในอัตราดอกเบี้ยต่ำ การเปลี่ยนแปลงในอัตราคิดลด เคยเป็น สำคัญกว่ามาก – โดยเฉพาะอย่างยิ่งสำหรับบริษัทที่ไม่จ่ายเงินปันผล ดังนั้นพวกเขาจึงเห็นคุณค่าของการเก็บเกี่ยวในอนาคตอันไกลโพ้น – มากกว่าการเปลี่ยนแปลงโชคชะตาของบริษัท
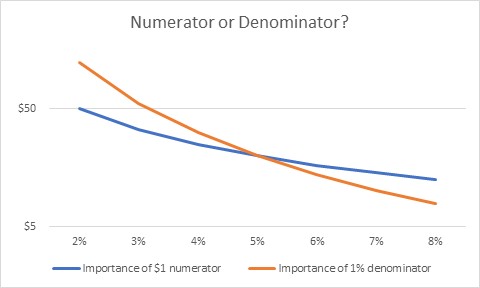
ตัวเศษเทียบกับ ตัวส่วน
อย่างไรก็ตาม เมื่อสิ่งนี้เป็นจริงน้อยลง เมื่ออัตราดอกเบี้ยสูงขึ้น นักลงทุนควรเริ่มสนใจเกี่ยวกับการพัฒนาของบริษัทมากขึ้นเรื่อยๆ ฉันไม่รู้ว่ามีเวทย์มนตร์อะไรเกี่ยวกับครอสโอเวอร์ 5% ที่ฉันมีในแผนภูมินั้น (แกน y เป็นลอการิทึมเพราะไม่เช่นนั้นเส้นสีส้มจะเป็นแนวตั้งเมื่อเราไปที่ขอบซ้าย!)
แต่สำหรับผมแล้ว การเลือกหุ้นเมื่ออัตราดอกเบี้ยต่ำนั้นอาจไร้ประโยชน์ ในขณะที่การเลือกหุ้นเมื่ออัตราดอกเบี้ยสูงขึ้นนั้นน่าจะมีประโยชน์พอสมควร การพลาดรายได้หมายถึงอะไรเมื่ออัตราดอกเบี้ยอยู่ที่ศูนย์? น้อยกว่าการไม่ได้รับสายจาก Fed มาก แต่ที่ 5% การพลาดรายได้เป็นเรื่องใหญ่
บางทีบทความนี้อาจมีชื่อผิด ไม่ใช่ว่าตอนนี้เราทุกคนเป็นผู้ค้าตราสารหนี้ จนกระทั่งเมื่อไม่นานมานี้ เราทุกคนต่างก็เป็นผู้ค้าตราสารหนี้…แต่ความจริงก็น้อยลงเรื่อยๆ
และเป็นความจริงมากขึ้นเรื่อยๆ ที่การคาดการณ์การเติบโตของกำไรที่อ่อนแอสำหรับปีนี้และปีหน้า มีความสำคัญมากกว่าการคาดการณ์เดียวกันเมื่อสองปีที่แล้ว
แต่นักค้าตราสารหนี้ก็ยังเป็นเด็กที่เจ๋ง
***
- ฉันควรทราบด้วยว่า r > 0ซึ่งเป็นสิ่งที่เราไม่เคยต้องพูดกันมาก่อน ในพื้นที่เล็กน้อย อย่างไรก็ตาม มันคงเป็นเรื่องไร้สาระที่จะมีอัตราดอกเบี้ยติดลบตลอดเวลา หมายความว่ากระแสเงินสดในอนาคตมีค่ามากขึ้นเรื่อย ๆ … และความเป็นนิรันดร์นั้นมีค่าไม่สิ้นสุด
- นักสอนจะสังเกตว่าระยะเวลาที่ 2% ไม่ใช่การเปลี่ยนแปลงของค่าจาก 1% เป็น 2% หรือจาก 2% เป็น 3% แต่เป็นการเปลี่ยนแปลงทันทีที่ 2% โดยปรับขนาด 100bps แต่ขอย้ำอีกครั้ง ฉันไม่ได้พยายามทำโจทย์คณิตศาสตร์ให้ดี และแค่พยายามทำให้ประเด็นใหญ่ขึ้น
คำแนะนำการอ่านบทความนี้ : บางบทความในเว็บไซต์ ใช้ระบบแปลภาษาอัตโนมัติ คำศัพท์เฉพาะบางคำอาจจะทำให้ไม่เข้าใจ สามารถเปลี่ยนภาษาเว็บไซต์เป็นภาษาอังกฤษ หรือปรับเปลี่ยนภาษาในการใช้งานเว็บไซต์ได้ตามที่ถนัด บทความของเรารองรับการใช้งานได้หลากหลายภาษา หากใช้ระบบแปลภาษาที่เว็บไซต์ยังไม่เข้าใจ สามารถศึกษาเพิ่มเติมโดยคลิกลิ้งค์ที่มาของบทความนี้ตามลิ้งค์ที่อยู่ด้านล่างนี้
Source link





